The future of computer vision and machine learning is toward edge devices. This is why C++ matters. Following my previous post on simple and general tips to optimize C++ codes, I decided to explain further tips that are specified for implementing computer vision algorithms. There will be a series of tutorials focused on:

• Memory management (we are here!)

• SIMD and

• Parallel processing

Through these tutorials, we will see how we can implement a fast Gaussian smoothing function (just as an example) step-by-step. The 1^st step: clone the code, 2^nd step: read this post.

1. Memory is more important than computation

In the old days, computation was the main bottleneck of programs. This raised the need to have faster processors. The size of transistors decreased and processors became faster but memory didn’t improve in that rate. If you need really fast code, you have to take care about allocations, alignment, cache misses, and stuffs like that.

2. Levels of memory

Before digging into the tips, I want you to carefully look at this figure to see what is going on under the hood.

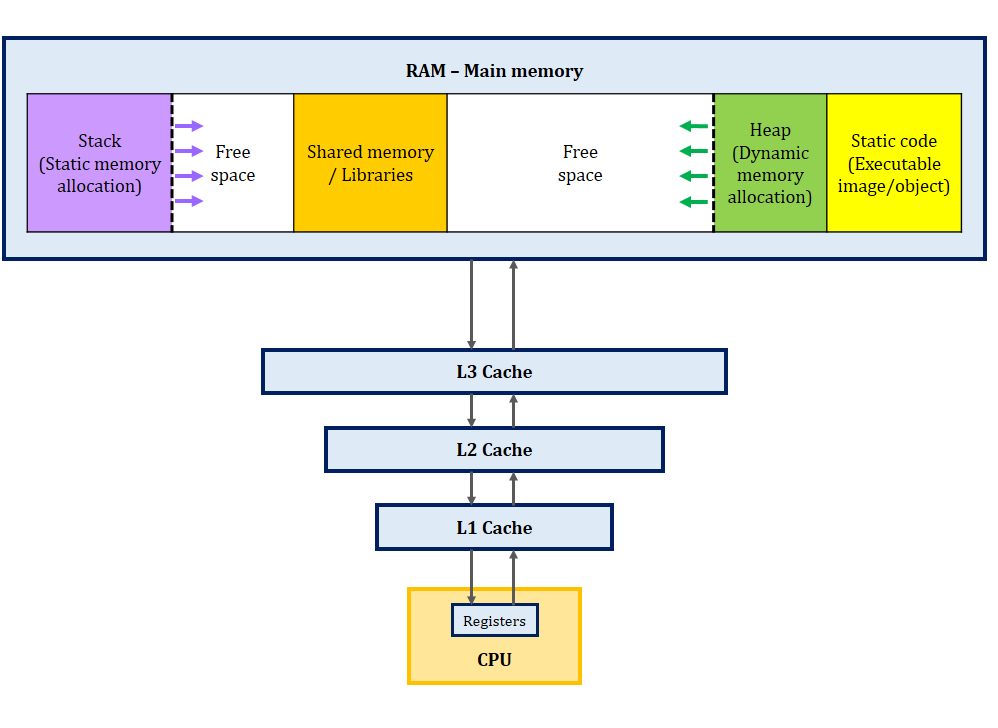
The CPU doesn’t access the data directly. There is a hierarchy in which the closer memories are smaller and faster. This hardware design implies that the workflow of your software should be designed in a way that uses those smaller memories as much as possible. Otherwise, the CPU remains idle, waiting for the data to be fetched from slower memories. With this picture in mind, let’s see how we can design and implement fast image processing codes.

3. Heap or Stack?

There are 2 main types of RAM memory to store images: Stack and Heap. Stack is accessed much faster than heap. If your application doesn’t consist of loading and storing several high resolution images, then use stack by simply defining a 2D static array:

unsigned char image[rows][cols];

But in most cases, stack can’t be used. Suppose that you want to implement a scale-space for a multi-scale algorithm. Stack will soon overflow due to its limited size. You need a much larger memory. That’s where you must use heap. But how to efficiently allocate memory in heap?

4. Forget about using 2-D std::vector

Basically, we prefer a container that can be easily passed/returned to functions. We also want to easily get the number of rows and columns everywhere we wish. The first and the easiest method to have such a container is to use 2D vectors. You can easily pass and return them in functions. Also, there are lots of STL methods that can make life easier for you. BUT, don’t use them. They are slow because:

• Vectors were invented to handle dynamic size storage. Their allocation/deallocation takes extra time to check some stuff related to this dynamic property.

• Pixels in each row are allocated continuously but rows themselves are not continuous with respect to each other. This makes the CPU to access the rows with much more effort compared to a continuous memory.

The first issue can be resolved by using 2D arrays. Their sizes are static. But 2D arrays are not continuous too. Moreover, passing/returning them as well as getting their rows and columns requires some dirty codes which we don’t prefer to use.

5. Continuous 1-D allocation

Surely, a continuous 1-D array is a good way to store an image. It’s very cache-friendly. But a 1-D array takes just one index for accessing a pixel. We prefer to access the pixels with their row and column addresses. One solution is to define a class, and use operator overloading to access a pixel. Check a sample implementation here.

But there is a better solution. Operator overloading requires a multiplication and an addition each time we want to access a pixel. This will soon slow down your code. The best solution is

“This Matrix class”

Let me explain it. First, there are some functions and operator overloadings to make routine things easier. Quite clear. I will skip them. Then, there are three important public variables. One to save the number of columns, another for saving the number of rows, and a pointer of pointers to save the pixels. This is the key to efficiency. Look what happens when calling allocatememory

void allocateMemory (const unsigned m, const unsigned n)
{
    rows = m;
    cols = n;
    if (m==0 || n==0)
    {
        val = 0;
        return;
    }
    val    = (T**)malloc(m*sizeof(T*));
    val[0] = (T*)malloc(m*n*sizeof(T));
    for(unsigned i=1; i<m; i++)
        val[i] = val[i-1]+n;
}

First, an array of pointers are defined using malloc. Then, the first element of this array is allocated again by malloc to store the whole array in 1-D. Other elements, just point to the rows of the matrix. Bingo! We have a 1-D array that stores the whole data (first element) but can access it as a 2-D array using [][] operators.

6. What about alignment?

Alignment means that the memory address of each pixel would be dividable to its size (check this video). For example, if the image is going to store 8bit pixels, then their addresses must be dividable by 8. If the data is not aligned, then the CPU (usually the old ones) has to do more things to load the pixels. The good news is that malloccares about alignment. It provides an aligned block of memory for almost every basic type that you may use for storing your images (unsigned char, int, float, double, etc.). If you need a custom datatype, then use posix_memalign.

7. Gaussian smoothing

Okay…now that we have found an efficient way to store and use the images, let’s implement one of the basic building blocks of computer vision algorithms: Gaussian smoothing.

For simplicity, I assume the kernel size to be 5×5 and the sigma value to be 1.

First of all, I need to pad the image because later the sliding window reaches the image borders and we don’t have pixels there! There are different policies for padding. I chose the replication mode.

The padded image is now ready to be convolved by the Gaussian kernel. The filter is separable and I defined two functions. One to do horizontal convolution, and the other to do vertical.

Finish :)

It works. But running the code on Raspberry Pi 3B+ (32bit OS, GCC 6.3) shows that OpenCV does this much much faster :

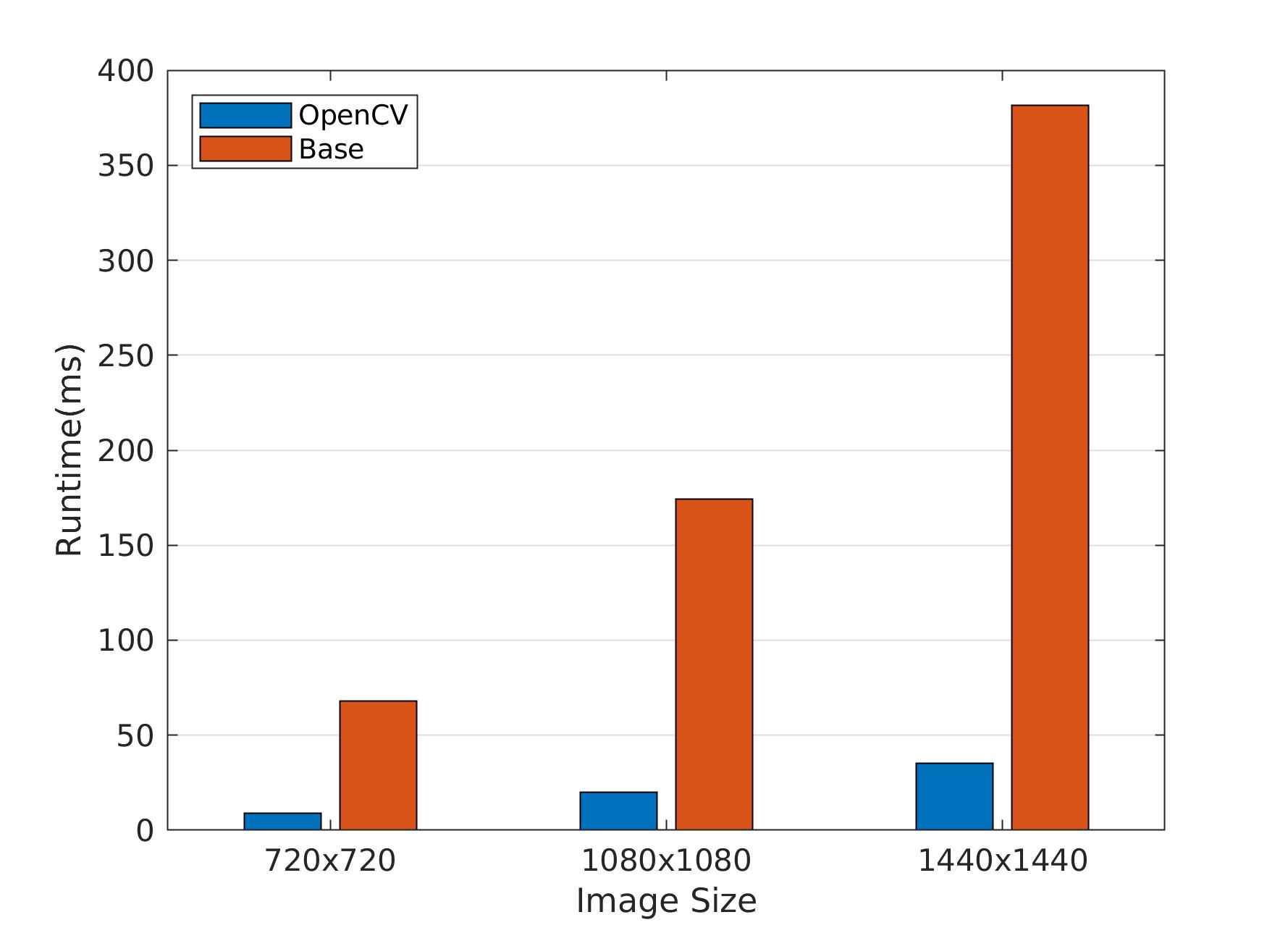
Let’s see what can we do.

7-1. Refinement #1: Write cache-friendly code

Cache is almost the closest memory to CPU. When you access a pixel, the CPU predicts that its neighbor pixels would be soon used in the code. So it loads the whole image row into the cache to accelerate the access of other pixels in that row. Now, imagine that a programmer wants to access the pixels column-wise. Pixel[0][0] is accessed and the CPU loads the first image row into the cache. Then, the code calls pixel[1][0]. The first image row which was loaded into the cache is thrown away and the second row is loaded instead. Next, the code calls pixel[2][0]. Again the second image row which was loaded into the cache is thrown away and the third row is loaded instead. Every time that the code request for a new pixel, the previous loaded row is thrown away from the cache. This is called cache-miss. Avoid cache-miss as much as you can. See the difference in run-times.

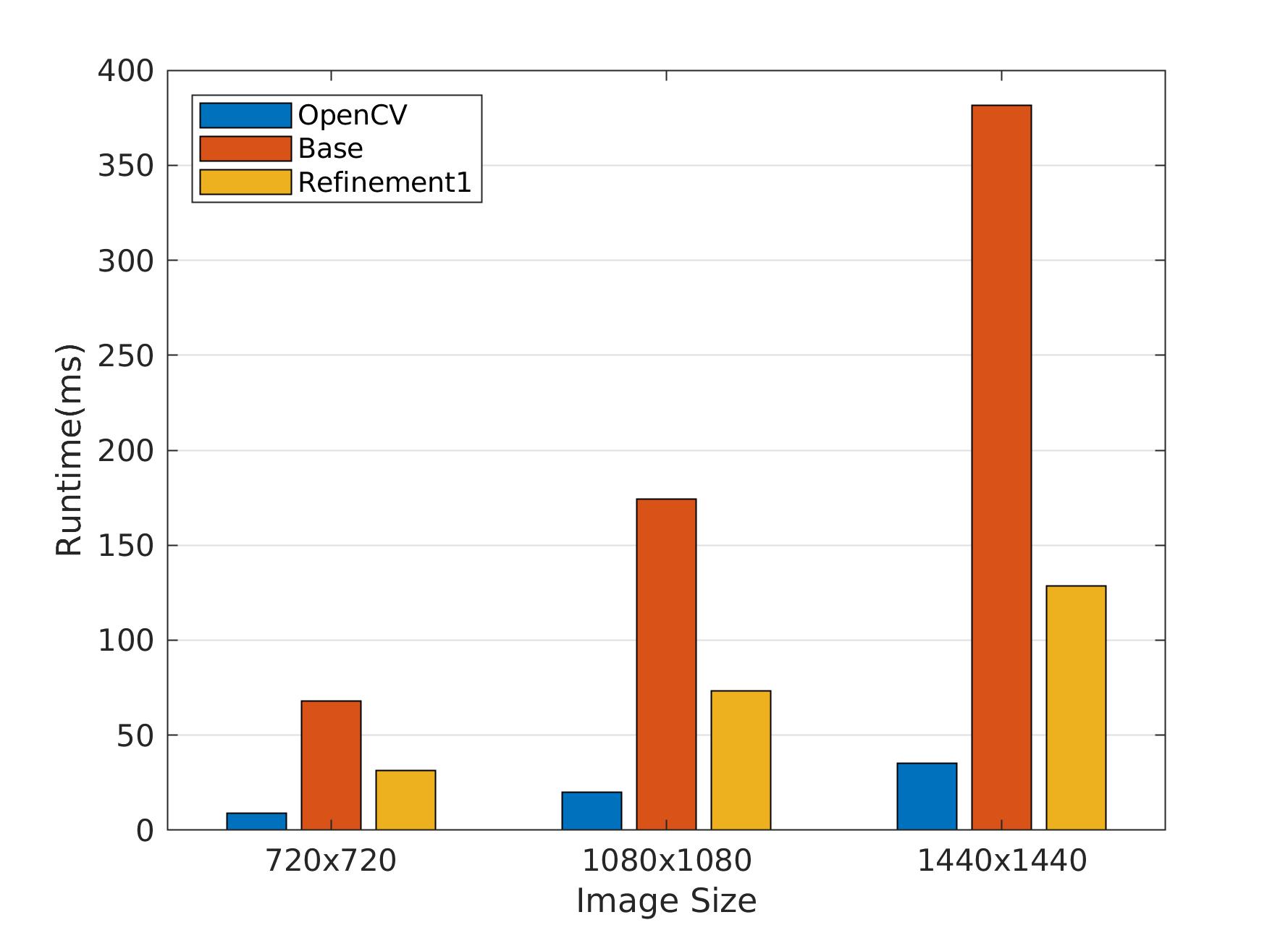
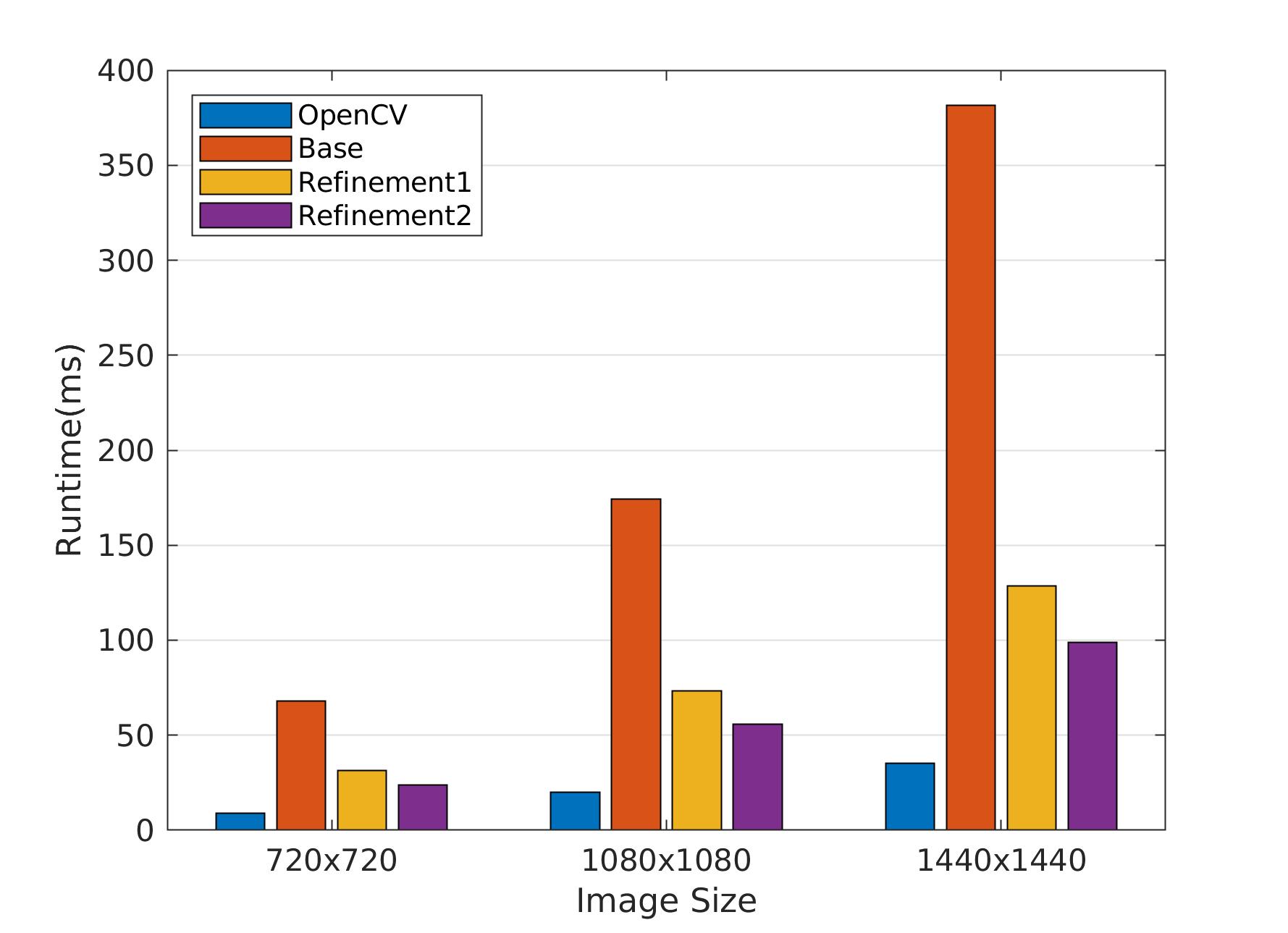
7-2. Refinement #2: Avoid padding

Have you thought about padding? To have that padded image, you must allocate a new image on the heap, and copy the 99% of your source image to it. Then fill the borders based on the padding policy. Copying all those pixels kills the performance. We can do much much better if we define separate convolution formulas for left and right columns, as well as top and bottom rows. See the gain with different image sizes.

7-3. Refinement #3: Use buffers in stack

Gaussian filter is separable. So, I first applied the convolution vertically, saved the result in a temporary image and then applied a horizontal convolution on that temporary image to get the Gaussian-blurred image. Seems good. But it can be faster. Bear this in mind:

“Writing to heap memory costs a lot. Minimize it.”

In this case, we can get rid of that temporary image (which is allocated on heap) and use a static 1-D array instead. Actually, we apply vertical convolution to calculate a row, store that row in the 1-D buffer in stack, and then apply horizontal convolution on that buffer to get a row of the Gaussian-blurred image. See the gain with different image sizes.

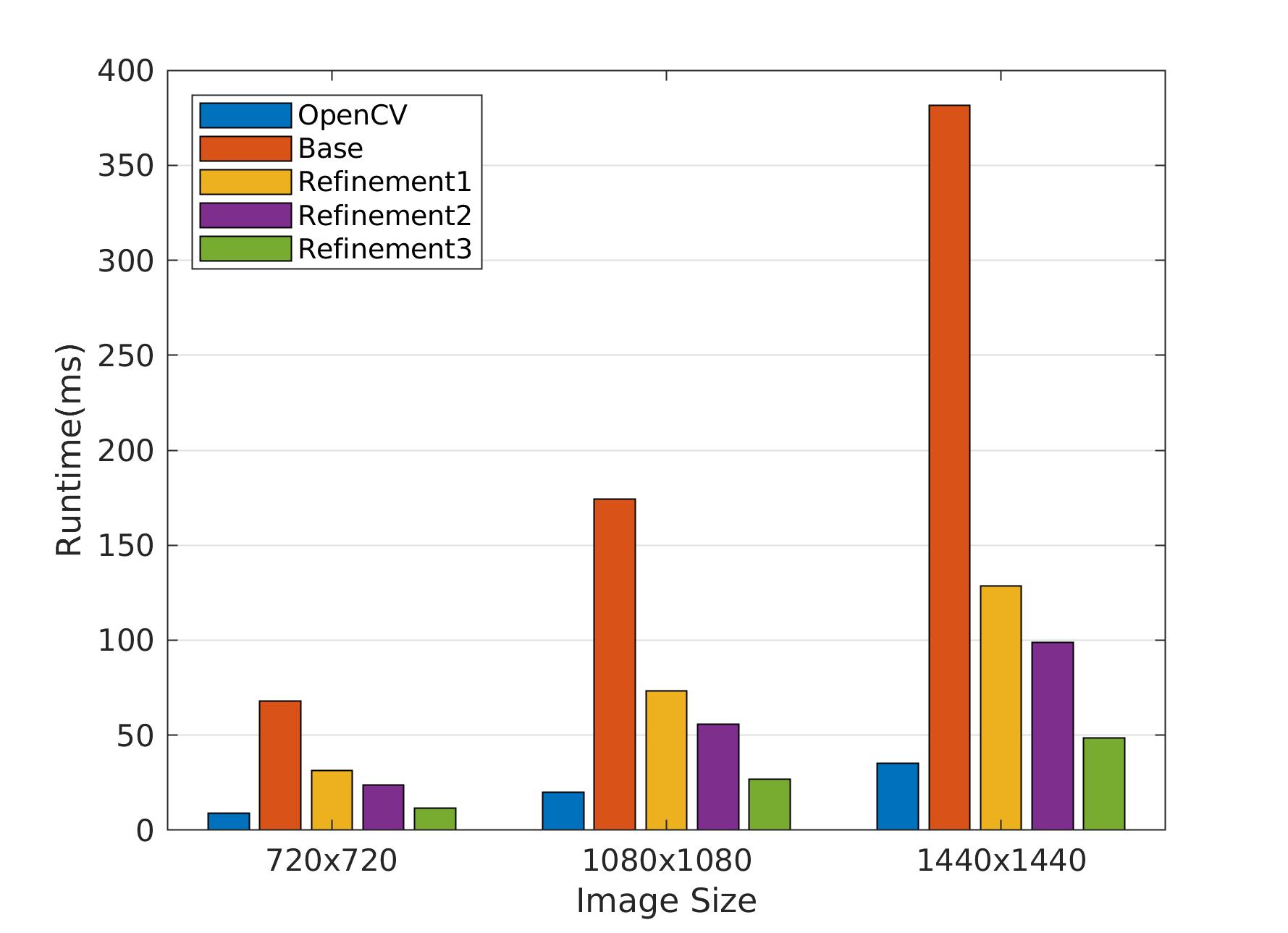
8- Summary

• The way you use memory can make huge differences in terms of efficiency.
• The first step is to use a good container. 1-D continuous array is a good choice for images.
• Access the pixels row-wise or column-wise (depending on how they are stored in the container) to avoid cache misses.
• Avoid padding in convolutions
• Use stack instead of heap to store temporary images